Addition-chain Exponentiation Algorithm
Of the modular exponentiation in advance because E is known previously. The shortest addition-chain algorithm requires no more multiplications than binary exponentiation and usually less.
 Evolutionary Programming For The Length Minimization Of Addition Chains Sciencedirect
Evolutionary Programming For The Length Minimization Of Addition Chains Sciencedirect
CiteSeerX - Document Details Isaac Councill Lee Giles Pradeep Teregowda.
Addition-chain exponentiation algorithm. For an RSA implemented with the Chinese Remainder Theorem method one faulty execution suffices to factorize the public modulus and. 2r max L r holds trivally. M r med L r μ r the arithmetric average of numbers which have a shortest addition chain of length r.
Brauer chain is a sac for n 12509. Genetic Algorithm Modular Multiplication Cipher Text Modular Exponentiation Addition Chain These keywords were added by machine and not by the authors. A Brauer chain aka star-chain is an addition chain where each new element is formed as the sum of the previous element and some element possibly the same.
Chain found by the algorithm is an optimal addition chain and it does not ne ed too much space. It uses the fact that this exponentiation algorithm works with a pair of intermediate variables a 0a 1 storing values of the form mαmα1. At the end of the exponentiation the pair a 0a 1 equals md1md and the consistency of the computation can be verified by checking wether a 0 m equals a 1.
The Euclidean method was first introduced in Efficient exponentiation using precomputation and vector addition chains by PD Rooij. This process is experimental and the keywords may be updated as the learning algorithm improves. The best method for exponentiation depends strongly on the group being used the hardware the.
A satisfying bk-. In practice therefore shortest addition-chain exponentiation is primarily used for small fixed exponents for which a shortest chain can be precomputed and is not too large. If aiai-1 ak is called a star step.
An addition chain exponentiation may require an important amoun t of memory to store the intermediate powers required for the computation of subsequen t powers. As such it would be nice to have a list for the small powers already computed. Addition chain-based exponentiation methods are used to find a sequence of elements in a given multiplicative group G such that the first number is 1 G and the last is s for some arbitrary s2G and 2Z.
Ask Question Asked 9 years 3 months ago. M r the median of numbers which have a shortest addition chain of length r. For any given target the number of large steps is fixed by n.
Even given a shortest chain addition-chain exponentiation requires more memory than the binary method because it must potentially store many previous exponents from the chain simultaneously. More generally addition-chain exponentiation may also refer to exponentiation by non-minimal addition chains constructed by a variety of algorithms since a shortest addition chain is very difficult to find. 1 the first number is one 2 every element is the sum of two earlier elements and 3 the given number occurs at the end of the sequence.
It is extremely popular. λ ai λ ai-1 and we call this a small step. The algorithm uses wh-2 multiplications and w1 elements must be stored to compute x n see.
Again for step i we say that. Where I set the initial upper limit at the number of multiplications it would take the normal binary squaremultiply algorithm and it does give the right answers but Im not satisfied with the running time it can take several seconds for numbers around 200. An addition-chain of length 1 for an integer n is a sequence of integers ao a1.
In mathematics and computer science optimal addition-chain exponentiation is a method of exponentiation by positive integer powers that requires a minimal number of multiplications. The largest number which has an addition chain of length r. Given a natural number e an addition chain AC for e is a finite sequence of numbers having three properties.
It works by creating a shortest addition chain that generates the desired exponent. If ai2ai-1 is called a doubling. An addition-chain is used to represent the sequence which is defined as follows.
The question of finding the Minimal Addition Chain MAC for needed for Addition chain exponentiation seems to be NP-complete. If a fault is injected during the computation the coherence between a. So finding an optimal addition chain amounts to finding a chain with minimal small steps.
C r min L r 2r. Fault Analysis is a powerful cryptanalytic technique that enables to break cryptographic implementations embedded in portable devices more efficiently than any other technique. Brauers algorithm is often called the left-to-right 2k-ary method or simply 2k-ary method.
The variable y is multiplied h-1 times with the initial u h-2 times with the next highest powers etc. Each exponentiation in the chain can be evaluated by multiplying two of the earlier exponentiation results.
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
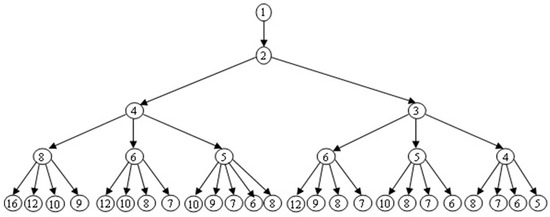 Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
 Pdf Generation Of Addition Chain Using Deterministic Division Based Method Semantic Scholar
Pdf Generation Of Addition Chain Using Deterministic Division Based Method Semantic Scholar
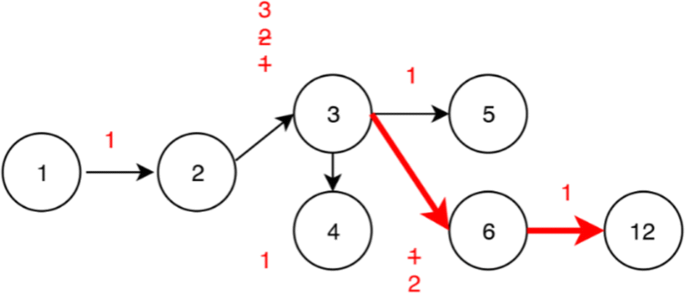
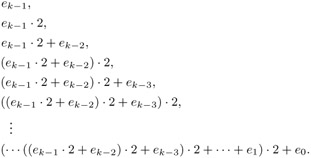 6 3 Addition Chains And Windows Cryptography In C And C
6 3 Addition Chains And Windows Cryptography In C And C
 A Hybrid Addition Chaining Based Light Weight Security Mechanism For Enhancing Quality Of Service In Iot Springerlink
A Hybrid Addition Chaining Based Light Weight Security Mechanism For Enhancing Quality Of Service In Iot Springerlink
Https Www Ams Org Mcom 1986 46 174 S0025 5718 1986 0829630 0 S0025 5718 1986 0829630 0 Pdf
 Project Euler 122 Most Efficient Exponentiation Method Mathblog
Project Euler 122 Most Efficient Exponentiation Method Mathblog
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
 Comparison Of The Average Length Of The Addition Chains Download Scientific Diagram
Comparison Of The Average Length Of The Addition Chains Download Scientific Diagram
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
 Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
Computers Free Full Text An Efficient Multicore Algorithm For Minimal Length Addition Chains Html
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar
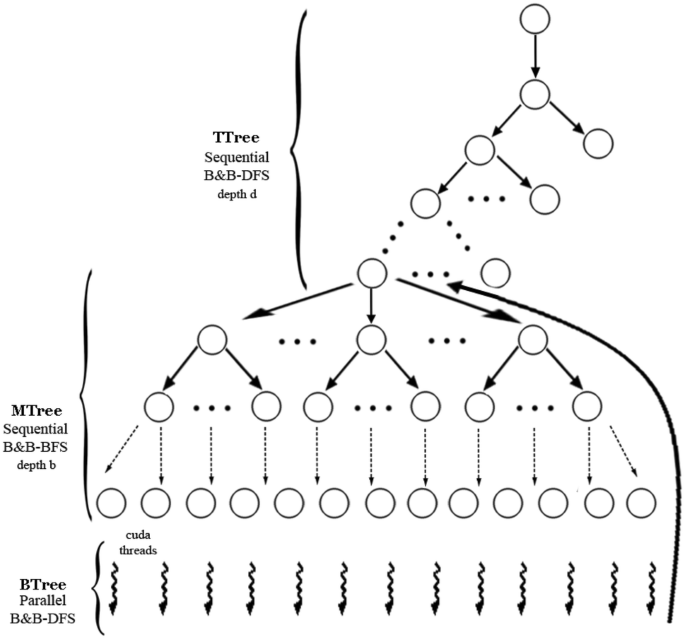 A Fast Gpu Based Hybrid Algorithm For Addition Chains Springerlink
A Fast Gpu Based Hybrid Algorithm For Addition Chains Springerlink
 Addition Chain Exponentiation Semantic Scholar
Addition Chain Exponentiation Semantic Scholar