Binary Floating Point Addition Algorithm
As a case in point lets use decimal instead of float and assume 3 digits of precision. Shift the mantissa of X m by Ye - Xe steps to the right to form X m 2 Ye-Xe if Xe is smaller than Ye else the mantissa of Y m will have to be adjusted.
 Floating Point Arithmetic Unit Computer Architecture
Floating Point Arithmetic Unit Computer Architecture
For example in the number 111011 x 2 3 the sign is positive the mantissa is 111011 and the exponent is 3.

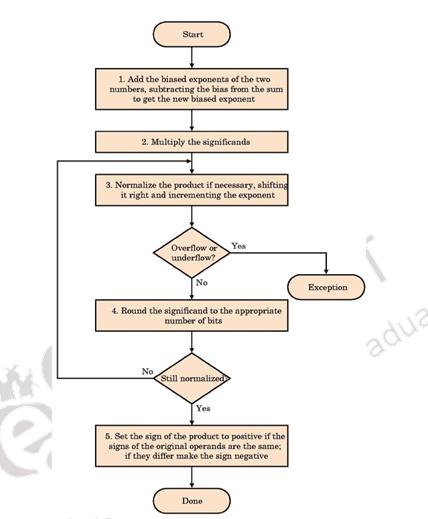
Binary floating point addition algorithm. Result X Y Xm x 2 Xe Ym x 2 Ye. Align decimal points Shift number with smaller exponent 9999 101 1 0016 10 2. FLOATING POINT ADDITION AND SUBTRACTION.
Also sum is not normalized 3. Thus the first number becomes 0225x. Compute X m 2 Ye-Xe Y m.
Floating-Point Addition Consider a 4-digit decimal example 9999 101 1610 10 1 1. The algorithm for Floating Point AdditionSubtraction consists of the following steps. Normalize result check for overunderflow 10015 102 4.
Add or subtract the mantissas. Given that add together the following 3 numbers. All positional base-N number systems share this problem with precision Plain old decimal base 10 numbers have the same issues which is why numbers like 13 end up as 0333333333.
IEEE 754 standard floating point Addition Algorithm. In our example it is expressed as. Add the numbers with decimal points aligned.
The exact sum is 100500000000100 which rounded to 3 digits is 101. 1011 12 04 18 116. Converting from the array of partials back to a single floating-point value was not discussed in the paper.
Addition and subtraction During addition and subtraction the two floating point operands are in AC and BR. What Every Computer Scientist Should Know About Floating-Point Arithmetic floating-point-guide Side Note. I have followed some example algorithms that I have found online and a good number of test cases match against a proven software implementation.
In this video we have discussed about how the floating point addition in Arithmetic Pipeline takes placeStep by Step evaluation have been shown with Algorit. Basic Floating Point Addition Algorithm Assuming that the operands are already in the IEEE 754 format performing floating point addition. Round and renormalize if necessary.
Im trying to understand IEEE 754 floating point addition at a binary level. Once the decimal points are aligned the addition can be performed by ignoring the decimal. A binary floating-point number is similar.
Align the mantissas ie right shift the significand of the smaller operand by d bits. For example we have to add 11 10 3 and 50. If the numbers are of opposite sign must do subtraction.
Allign decimal point of number with smaller exponent 1610 10-1 0161 100 00161 101 Shift smaller number to right 2. Compute Ye - Xe a fixed point subtraction. Shift the decimal point of the smaller number to the left until the exponents are equal.
One digit of precision lost during shifting. My algorithm is only dealing with positive numbers at the moment. The algorithm can be divided into four consecutive parts.
Add significands 9999 101 0016 101 10015 101 3. This chapter is a short introduction to the used notation and important aspects of the binary floating-point arithmetic as defined in the most recent IEEE 754-2008A more comprehensive introduction including non-binary floating-point arithmetic is given in Brisebarre2010 Chapters 2 and 3. Floating Point Addition Example 1.
Floating-point addition is more complex than multiplication brief overview of floating point addition algorithm have been explained below X3 X1 X2 X3 M1 x 2 E1 - M2 x 2 E2 1 X1 and X2 can only be added if the exponents are the. Let X and Y be the FP numbers involved in additionsubtraction where Y e X e. The fractional portion of the mantissa is the sum of successive powers of 2.
Add significands 9999 0016 1 NOTE. However I am not getting a match with this test case. To understand floating point addition first we see addition of real numbers in decimal as same logic is applied in both cases.
Arithmetic operations on floating point numbers consist of addition subtraction multiplication and division. Check for special values on inputs. The sum of difference is formed in the AC.
The operations are done with algorithms similar to those used on sign magnitude integers because of the similarity of representation example only add numbers of the same sign.
 Block Diagram Of The Proposed Floating Point Addition Algorithm Download Scientific Diagram
Block Diagram Of The Proposed Floating Point Addition Algorithm Download Scientific Diagram
 Floating Point Addition Example Youtube
Floating Point Addition Example Youtube
 Binary 8 Floating Point Binary Subtraction Youtube
Binary 8 Floating Point Binary Subtraction Youtube

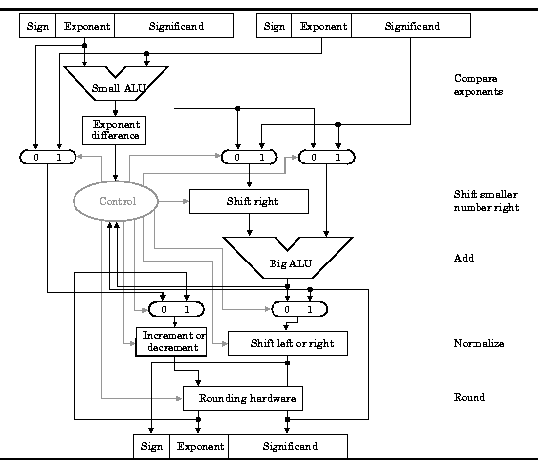
 Organization Of Computer Systems Computer Arithmetic
Organization Of Computer Systems Computer Arithmetic
 An Algorithm To Convert Float Number To Binary Representation Mathematics Stack Exchange
An Algorithm To Convert Float Number To Binary Representation Mathematics Stack Exchange
 Block Diagram Of The Proposed Floating Point Addition Algorithm Download Scientific Diagram
Block Diagram Of The Proposed Floating Point Addition Algorithm Download Scientific Diagram
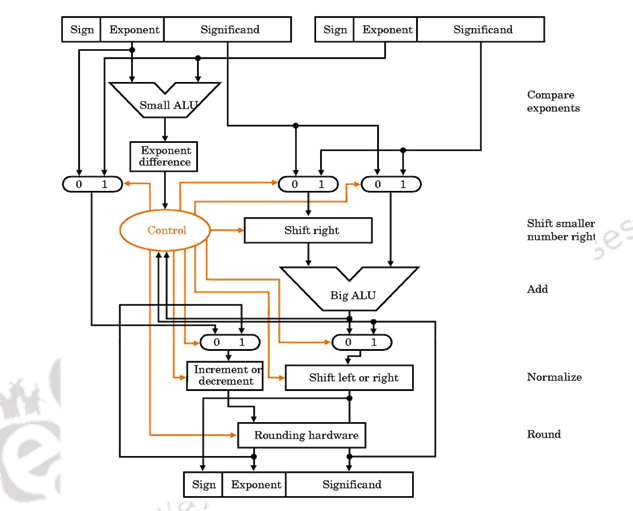
 Organization Of Computer Systems Computer Arithmetic
Organization Of Computer Systems Computer Arithmetic
 Floating Point Addition And Subtraction Youtube
Floating Point Addition And Subtraction Youtube
 Floating Point Arithmetic Unit Computer Architecture
Floating Point Arithmetic Unit Computer Architecture
 Algorithm For Floating Point Addition Subtraction Download Scientific Diagram
Algorithm For Floating Point Addition Subtraction Download Scientific Diagram
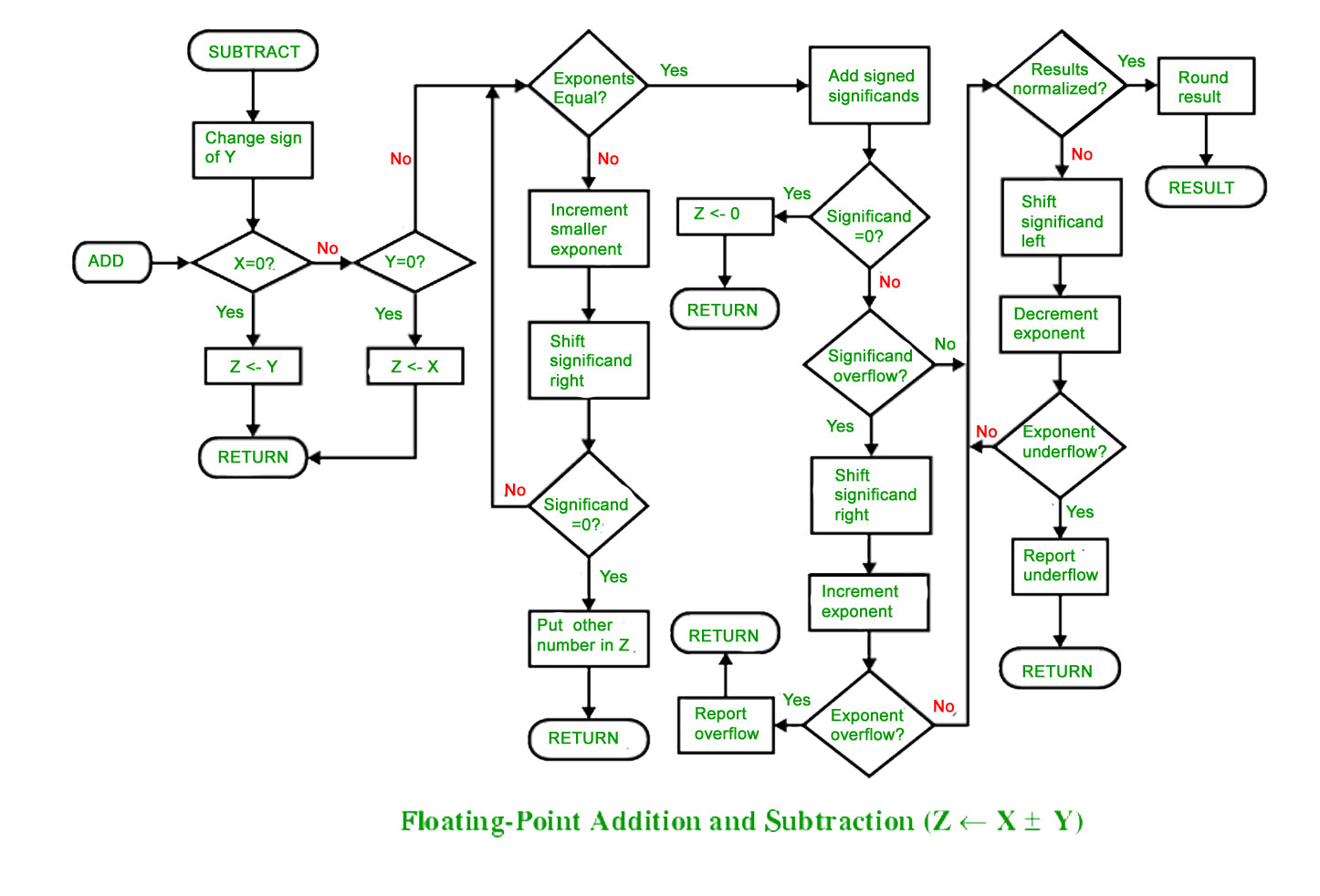 Computer Arithmetic Set 2 Geeksforgeeks
Computer Arithmetic Set 2 Geeksforgeeks
 Floating Point Addition And Subtraction Youtube
Floating Point Addition And Subtraction Youtube
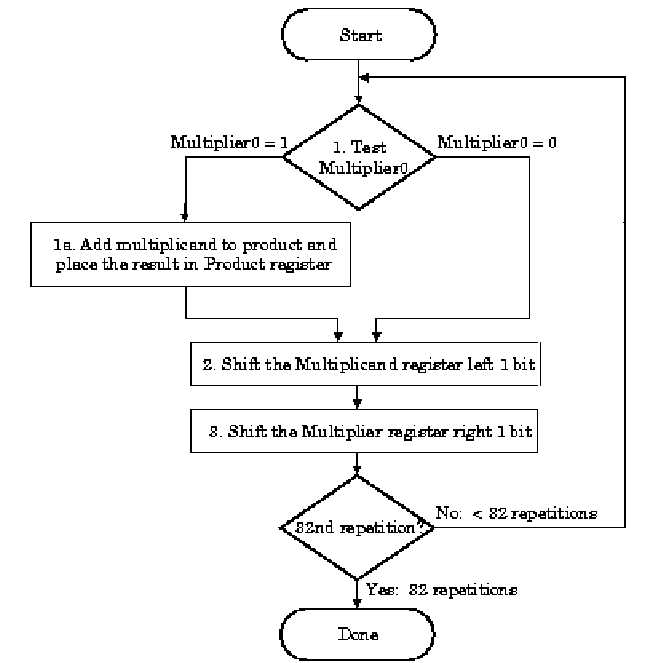
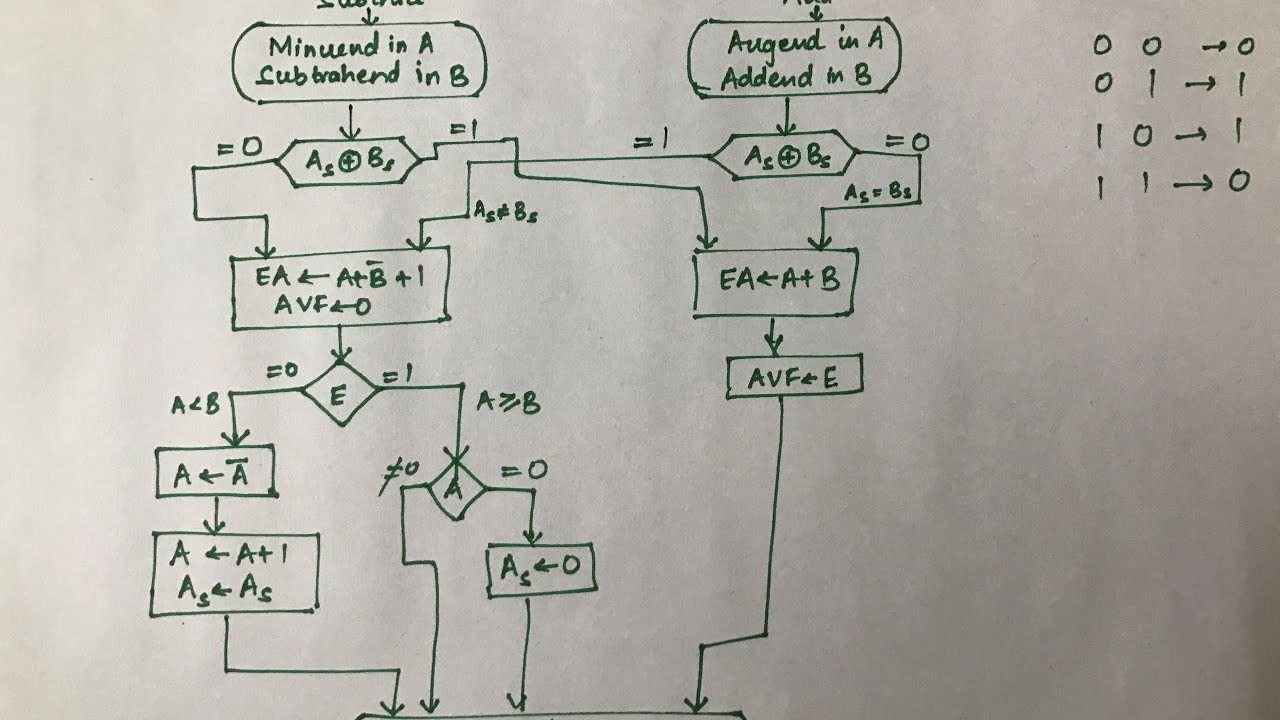 Addition And Subtraction Binary Arithmetic Part 2 Youtube
Addition And Subtraction Binary Arithmetic Part 2 Youtube
 Algorithm For Floating Point Addition Subtraction Download Scientific Diagram
Algorithm For Floating Point Addition Subtraction Download Scientific Diagram

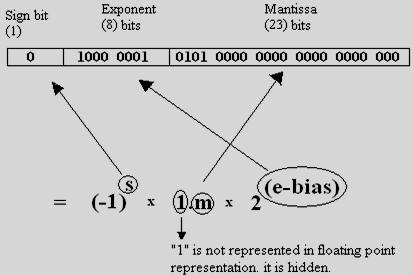 Floating Point Tutorial Ieee 754 Floating Point Basics Tutorials
Floating Point Tutorial Ieee 754 Floating Point Basics Tutorials
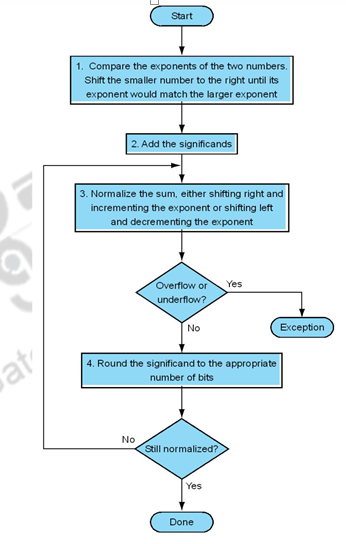 Floating Point Arithmetic Unit Computer Architecture
Floating Point Arithmetic Unit Computer Architecture
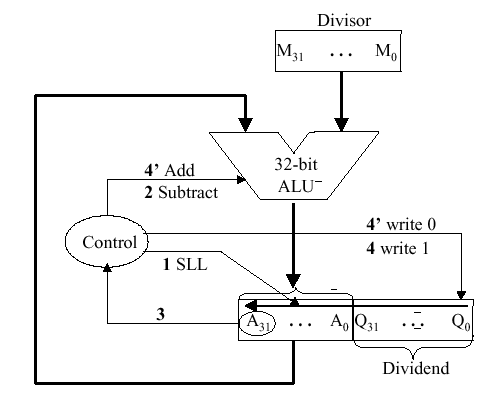 Organization Of Computer Systems Computer Arithmetic
Organization Of Computer Systems Computer Arithmetic